Missing matter

The current framework of fundamental physics, called the Standard Model (SM), has successfully withstood every laboratory test. Furthermore, with the discovery of the Higgs particle in 2012, every core prediction of the SM has been validated by experiment. Despite these successes, the SM alone cannot explain the entirety of fundamental physics. Perhaps most dramatically, astronomical observations over the last fifty years have shown that only 15% of the matter in the universe is composed of particles described by the SM. The remaining particles, which do not (or only very weakly) interact with light, are known as “dark” matter. Very little is known with certainty about the nature of dark matter.

One major source of evidence for dark matter is gravitational lensing (see right), where the path of light from distant galaxies is bent by the gravitational in uence of galaxies in the cosmic neighborhood of its trajectory. As a result, images of the night sky become distorted. By analyzing the distortions, it is possible to infer the positions and masses of the gravitational sources. This method produces the most accurate maps of the matter density throughout the universe. Remarkably, these maps show that all visible matter comprises only a small fraction of all matter. The difference is “dark matter,” which is gravitationally active but does not emit or absorb light. Simulations of nucleosynthesis and cosmological structure formation as well as observations of the cosmic microwave background are also consistent with a universe composed of 85% dark matter [1].

Polyatomic molecules as dark matter sensors

In many well-motivated models, cold dark matter particles behave collectively like a classical field throughout space (such as a gravitational field) [2]. Such a dark matter field would oscillate at a frequency determined by the mass of each particle. Depending on its interactions with ordinary matter, electrons and nuclei would undergo a slight change in mass that follows the oscillation of the dark matter field. Thus high-precision measurements of fundamental “constants,” such as the ratio of electron mass to prooton mass, could reveal a small time-dependence. The magnitude of this time-dependent part of the fundamental constant contains information about the interactions between dark matter and ordinary matter, while the frequency of oscillation would reveal the dark matter particle mass.

Energy oscillation

The energies of molecular vibrations and rotations depend on the proton-to-electron mass ratio, denoted by μ: for example, increasing the proton mass (with the electron mass fixed) reduces the energy of a rotating or vibrating molecule. The fractional change in the energy of a rotating or vibrating molecule is typically the same (within a factor of two) as the fractional change in μ. However, absolute energies of individual states are not physically meaningful. Only energy differences can be measured. Certain special cases arise where the energies of two molecular states are nearly identical, but the states each have different fractional depenences on μ. In these cases, the dependence of the fractional energy difference on fractional changes in μ can be enhanced by a factor of hundreds to thousands! Oftentimes, experimental sensitivity is limited by systematic errors scaling with the absolute energy difference between two states (for example, due to technical noise sources in high-frequency radiation sources like lasers). Then, a larger fractional sensitivity of the transition can lead to a better ultimate absolute sensitivity to changes in μ.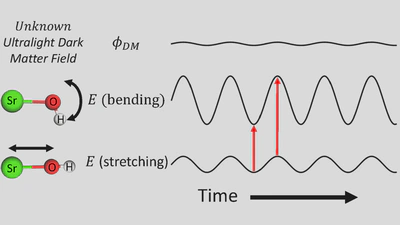

Laboratory-based dark matter detection with laser-cooled SrOH

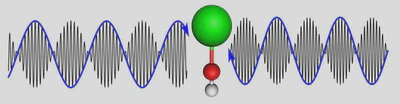
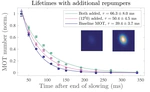
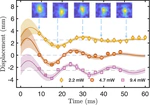
SrOH molecules were the first polyatomic molecules to be laser cooled, opening up the prospect of full quantum control over their internal states and trapping for long observation times [3]. There exists a pair of vibrational states in SrOH, namely a triply-excited bending vibration and a doubly-excited stretching vibration, with nearly the same energy but signicantly different dependences on μ. We have analyzed these states theoretically and found that a transition between them can be driven by microwave radiation, and their energy difference thereby directly measured [4]. Microwave-scale energies are more straightforwardly measured to high precision (e.g., compared to an optical-energy measurement using a frequency comb), and the small scale of the energy difference between the states suppresses potential systematic errors. We have also identied sets of rotational states in the two vibrational manifolds that are expected to have nearly-zero common-mode sensitivity to electric and magnetic fields, leading to strong suppression of common systematic errors associated with imperfect control of electromagnetic elds. With one day of integration, we expect an absolute microwave frequency sensitivity of about 3 μHz for oscillation frequencies between about 10 μHz (bounded from below by the full one-day duration of the measurement) and 1 Hz (bounded from above by the coherence time of the vibrational states).

This range of oscillation frequencies allows us to probe dark matter particles with masses between 1×10−20 and 4×10−15 eV/c2, which is a range of signicant theoretical interest in cosmological particle physics. With this sensitivity, we expect to probe new parameter space on beyond-the-Standard-Model particles such as dilatons (see right) to either rule out signicant parameter-space of such theories or discover the microscopic nature of dark matter.

References

[1] Katherine Garrett, Gintaras Duda, “Dark Matter: A Primer”, Advances in Astronomy, vol. 2011, Article ID 968283, 22 pages, 2011. https://doi.org/10.1155/2011/968283

[2] M. S. Safronova, D. Budker, D. DeMille, D. F. Jackson Kimball, A. Derevianko, C. W. Clark, “Searches for new physics with atoms and molecules,” Rev. Mod. Phys. 90 (2018). https://doi.org/10.1103/RevModPhys.90.025008

[3] I. Kozyryev, L. Baum, K. Matsuda, B. L. Augenbraun, L. Anderegg, A. P. Sedlack, and J. M. Doyle, “Sisyphus Laser Cooling of a Polyatomic Molecule” Phys. Rev. Lett. 118, 173201 (2017). https://doi.org/10.1103/PhysRevLett.118.173201

[4] I. Kozyryev, Z. D. Lasner, and J. M. Doyle, “Enhanced Sensitivity to Ultralight Bosonic Dark Matter in the Spectra of the Linear Radical SrOH,” arXiv:1805.08185